로딩 중이에요... 🐣
[코담]
웹개발·실전 프로젝트·AI까지, 파이썬·장고의 모든것을 담아낸 강의와 개발 노트
28 데이터분석 및 시각화 상관분석 | ✅ 저자: 이유정(박사)
상관분석이란? 변수들 간에 서로 어떤 관계가 있는지를 수치로 알아보는 분석이에요. 예를 들어:
- 나이가 많을수록 급여가 올라갈까?
- 시험 점수가 높을수록 연봉도 높을까? 이런 "함께 움직이는 정도"를 확인하는 게 상관분석(Correlation Analysis) 입니다.
상관계수 (Correlation Coefficient)
correlation_matrix = df[['age', 'salary', 'score']].corr()
| 상관계수 값 | 의미 |
|---|---|
| +1.0 | 완벽한 양의 상관관계 (둘 다 함께 증가) |
| 0.0 | 상관관계 없음 |
| -1.0 | 완벽한 음의 상관관계 (하나는 증가, 하나는 감소) |
| 예시: |
age와salary가 +0.7 이면 → 나이가 많을수록 급여가 높은 경향이 있다는 뜻score와salary가 -0.3 이면 → 점수가 높을수록 오히려 급여가 낮은 경향이 있다는 뜻
시각화로 상관관계 보기 히트맵 (Heatmap)
sns.heatmap(correlation_matrix, annot=True)
- 파란색: 음의 상관관계 (반대 방향)
- 빨간색: 양의 상관관계 (같은 방향)
- 숫자: 상관계수 어떤 변수들이 서로 강하게 관련되어 있는지 한눈에 볼 수 있어요.
산점도 (Scatter Plot)
sns.scatterplot(data=df, x='age', y='salary')
- 점들이 우상향이면 → 양의 상관관계
- 점들이 우하향이면 → 음의 상관관계
- 점들이 무질서하게 퍼져 있으면 → 관계 없음 변수 간 직접적인 분포와 경향성을 눈으로 확인할 수 있어요.
코드로 데이터 분석 및 시각화 해보기:
import pandas as pd
# CSV 파일에서 직원 데이터 불러오기
df = pd.read_csv("csv_files/employees_data.csv")
# 평균 (전체 급여의 합을 인원수로 나눈 값)
print("\nMean:") # 평균
print(df["salary"].mean())
# 중앙값 (정렬했을 때 한가운데 위치한 값)
print("\nMedian:") # 중앙값
print(df["salary"].median())
# 최빈값 (가장 많이 나타나는 값, 여러 개일 수도 있음)
print("\nMode:") # 최빈값
print(df["salary"].mode())
# 분산과 표준편차: 데이터의 퍼짐 정도를 나타냄
print("\nVariance, Standard Deviation:")
print(df["salary"].var())
#분산: 평균으로부터 값들이 얼마나 떨어져 있는지를 제곱해서 평균낸 값
print(df["salary"].std())
#표준편차: 분산의 제곱근, 원래 단위로 해석 가능
# 왜도와 첨도: 데이터 분포의 모양을 설명함
print("\nSkewness, Kurtosis:")
print(df["salary"].skew())
# 왜도: 값들이 한쪽으로 치우쳐 있는 정도 (0이면 대칭, 음수면 왼쪽, 양수면 오른쪽)
print(df["salary"].kurt())
# 첨도: 분포가 뾰족한지 평평한지를 나타냄 (0이면 정규분포와 유사, 양수면 뾰족, 음수면 평평)
결과값:
Mean: # 평균
89866.466
Median: # 중앙값
90171.0
Mode: # 최빈값
0 36445
1 104756
2 112293
3 121519
4 143795
5 144748
Name: salary, dtype: int64
Variance, Standard Deviation: # 분산과 표준편차
1216300260.6735175
34875.49656526079
Skewness, Kurtosis: # 왜도와 첨도
-0.0005633158265260066
-1.2256302046834466
시각화코드:
import seaborn as sns
import matplotlib.pyplot as plt
import pandas as pd
df = pd.read_csv("csv_files/employees_data.csv")
# change data type of age column to float
df['age'] = df['age'].astype(float)
df['salary'] = df['salary'].astype(float)
df['score'] = df['score'].astype(float)
correlation_matrix = df[['age', 'salary', 'score']].corr()
# 히트맵을 사용한 상관 계수 시각화
sns.heatmap(correlation_matrix, annot=True)
plt.show()
# 산점도를 사용한 두 변수 간 관계 시각화
sns.scatterplot(data=df, x='age', y='salary')
plt.show()
상관계수 행렬(correlation matrix) 을 시각화한 그래프
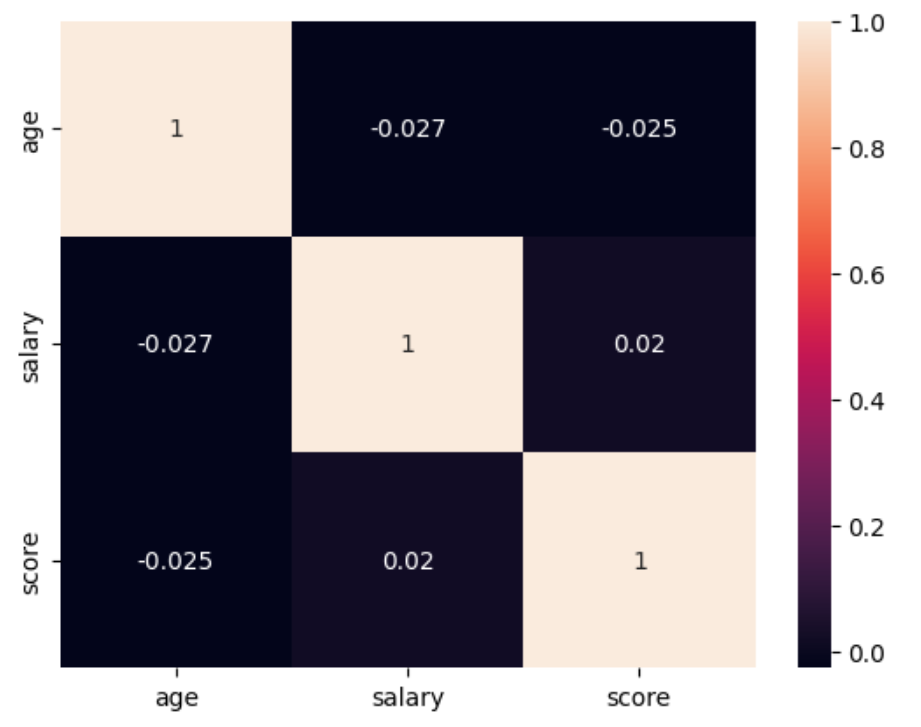 여러 변수들 간의 상관관계(서로 얼마나 관련이 있는지) 를 보여주는 표입니다.
축(X축과 Y축)
여러 변수들 간의 상관관계(서로 얼마나 관련이 있는지) 를 보여주는 표입니다.
축(X축과 Y축)
- 행(row) 과 열(column) 은 각각 변수(
age,salary,score)입니다. agevssalary,scorevssalary등을 비교합니다.
셀(Cell)의 숫자 = 상관계수 (correlation coefficient)
| 상관계수 값 | 의미 |
|---|---|
| +1.0 | 완전한 양의 상관관계 (서로 같이 증가) |
| 0.0 | 상관 없음 (무관함) |
| -1.0 | 완전한 음의 상관관계 (하나는 증가, 하나는 감소) |
| 즉, 살구색은 상관계수 1.0으로 자기 자신봐 비교했다는 의미로 항상 1이 나오며, | |
짙은 남색 (어두운색) 상관계수 ≈ 0 또는 ± 값 → 다른 변수와의 관계 정도를 나타내며 0에 가까우면 무관하다고 판단하면 된다. |
산점도란? 두 변수 사이의 관계를 점으로 표현한 그래프입니다. 이 산점도 해석하기
- x축:
age (나이) - y축:
salary (급여) - 하나의 점: 한 명의 직원 (나이와 급여 조합)
상관관계 산점도(Scatter Plot)
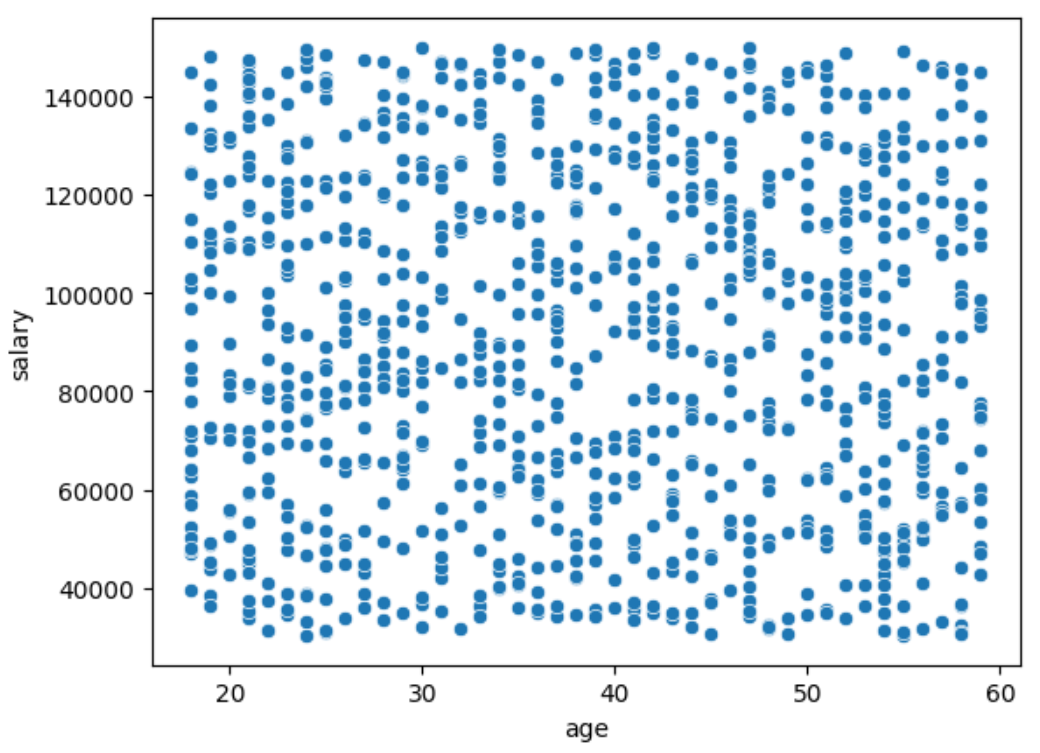
이 그래프를 통해 알 수 있는 것
| 관찰 포인트 | 설명 |
|---|---|
| 패턴 없음 | 점들이 특정 방향 없이 고르게 퍼져 있음 → 나이와 급여는 거의 상관이 없음 |
| 선형 관계 없음 | 나이가 많다고 해서 급여가 더 높은 것도, 적은 것도 아님 |
| 밀집도 일정 | 특정 구간에 몰림 없이 비교적 균등 분포되어 있음 |
- 이 산점도는
age와salary사이에 눈에 띄는 관계가 없다는 것을 보여줘요. - 실제로 상관계수가
-0.027로 거의 0에 가까워서 관계 없음이 수치로도 확인됩니다.
